บทที่ 3: การทำงานของเลขฐานสองในไมโครโปรเซสเซอร์
3.1 บทนำ
ในคอมพิวเตอร์ การดำเนินการทางคณิตศาสตร์จะดำเนินการใน 8 บิต, 16 บิต, 32 บิต หรือ 64 บิต ตัวเลขเช่น 3 ในไบนารี่คือ 11 หากต้องดำเนินการใน 8 บิต จะถือว่าเป็น 00000011 นำหน้าด้วย 0 ศูนย์
สำหรับเลขฐานสอง เช่น 10000101 บิตที่สำคัญที่สุดคือบิตทางซ้ายสุด ในกรณีนี้คือ 1 บิตที่มีนัยสำคัญน้อยที่สุดคือบิตสุดขีดทางด้านขวา ซึ่งยังคงเป็น 1 สำหรับตัวเลข บิตที่สำคัญที่สุดมีตัวย่อว่า MSB บิตที่มีนัยสำคัญน้อยที่สุดจะย่อว่า LSB
BInary digitiT ย่อว่า BIT และเขียนง่ายๆ ว่า bit ในหมายเลข 10010011 แต่ละตัวหรือศูนย์เป็นบิต กลุ่มสี่บิตเรียกว่าแทะ กลุ่มแปดบิตเรียกว่าไบต์ ไบต์ประกอบด้วยสองแทะ แทะด้านล่างคือแทะสำหรับ LSB และแทปที่สูงกว่าคือแทะสำหรับ MSB
กลุ่มของ 8 บิต, 16 บิต, 32 บิต หรือ 64 บิตเรียกว่าคำ ตราบใดที่กลุ่มนั้นถ่ายทอดข้อมูลนอกเหนือจากการระบุตัวเลข กลุ่มนี้เรียกว่าคำ เช่น ถ้าเป็นคำสั่งระดับต่ำในคอมพิวเตอร์ นอกจากนี้ยังมีคำขนาด 24 บิตด้วย แต่ปัจจุบันนี้ไม่ได้ใช้กันทั่วไป
Endianness หมายถึงลำดับที่ไบต์ประกอบเป็นคำ พิจารณาคำแบบ 24 บิต - 100100001111010100100010 คำนี้ประกอบด้วยสามไบต์ ได้แก่:
10010000 11110101 00100010
ไบต์ที่สำคัญที่สุดคือไบต์ซ้ายสุด เมื่อไบต์ทางซ้ายสุดเป็นไบต์ที่มีนัยสำคัญที่สุด และไบต์ทางด้านขวาสุดเป็นไบต์ที่มีนัยสำคัญน้อยที่สุด สิ่งนี้เรียกว่าการเป็นตัวแทนของคำ Big Endian การเป็นตัวแทนของ Little Endian นั้นตรงกันข้าม
หน่วยความจำคอมพิวเตอร์คือชุดของเซลล์ และแต่ละเซลล์เก็บไบต์ เซลล์แรกในหน่วยความจำของคอมพิวเตอร์คือเซลล์ 0 เซลล์ที่สองคือไบต์ 1 เซลล์ที่สามคือไบต์ 2 และอื่นๆ ด้วย big endianness และสำหรับคำก่อนหน้า ไบต์ที่สำคัญที่สุดจะถูกเก็บไว้ในเซลล์ไบต์ 0 ไบต์กลางจะถูกเก็บไว้ในเซลล์ไบต์ 1 และไบต์ที่มีนัยสำคัญน้อยที่สุดจะถูกเก็บไว้ในเซลล์ไบต์ 2 ซึ่งหมายความว่ามีไบต์ที่มีนัยสำคัญมากกว่าในเซลล์หน่วยความจำด้านล่าง
คำ 24 บิตก่อนหน้าสามารถเขียนในลำดับย้อนกลับของไบต์ได้ดังนี้:
00100010 11110101 10010000
ตอนนี้ ไบต์ที่มีนัยสำคัญน้อยที่สุดจะอยู่ที่ด้านซ้ายสุด และไบต์ที่มีนัยสำคัญที่สุดจะอยู่ทางด้านขวาสุด เมื่อไบต์ทางซ้ายสุดเป็นไบต์ที่มีนัยสำคัญน้อยที่สุด และไบต์ทางด้านขวาสุดเป็นไบต์ที่มีนัยสำคัญที่สุด คำนี้จะเป็นตัวแทนของ Little Endian ไบต์ที่มีนัยสำคัญน้อยที่สุดจะถูกเก็บไว้ในเซลล์ไบต์ 0 ไบต์กลางจะถูกเก็บไว้ในเซลล์ไบต์ 1 และไบต์ที่สำคัญที่สุดจะถูกเก็บไว้ในเซลล์ไบต์ 2 ซึ่งหมายความว่ามีไบต์ที่มีนัยสำคัญน้อยกว่าในเซลล์หน่วยความจำด้านล่าง
Endianness ไม่ได้ใช้สำหรับบิตในหน่วยไบต์ นอกจากนี้ยังไม่ได้ใช้สำหรับการแทะในหน่วยไบต์ ใช้สำหรับลำดับไบต์เท่านั้น
เส้นจำนวน
จำนวนที่ไม่มีเครื่องหมายจะเป็นจำนวนบวก ตัวเลขบวกคือตัวเลขตั้งแต่ศูนย์ขึ้นไป ตัวเลขติดลบก็มีอยู่เช่นกัน จำนวนบวกและลบสามารถแสดงบนเส้นจำนวนได้ เส้นจำนวนต่อไปนี้แสดงจำนวนเต็มบวกและลบ (จำนวนเต็ม) ใกล้ศูนย์:
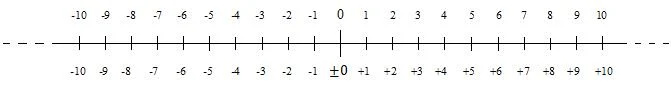
จำนวนลบลดลงจากศูนย์ลง (ซ้าย) ในหลาย ๆ สถานการณ์ ค่าศูนย์ถือเป็นค่าบวก อย่างไรก็ตาม ก็ถือเป็นเชิงลบในบางสถานการณ์ นั่นคือสาเหตุว่าทำไมจึงมีเครื่องหมายบวกและลบอยู่หน้าศูนย์ในลำดับเลขล่างในแผนภาพ เมื่อตัวเลขเป็นค่าบวก ก็สามารถละเครื่องหมายได้ นี่เป็นกรณีของการกำหนดหมายเลขบนในแผนภาพ เครื่องหมายลบที่อยู่หน้าจำนวนลบจะไม่ถูกละไว้
3.2 การเพิ่มเลขฐานสอง
นอกจากนี้:
เอ + บี = ส
A เรียกว่า Augend B เรียกว่า Addend และ S เรียกว่าผลรวม
พิจารณาการบวกเลขบวกสองตัวในฐานสองดังต่อไปนี้:

ในฐานสอง ตัวเลขที่เป็นไปได้เพียงหลักเดียวคือ 0 และ 1 การบวกในฐาน 2 จะคล้ายกับการบวกในฐานสิบ แต่สองในฐานสองคือหนึ่งศูนย์ (10) เมื่อผลรวมของสองบิตในคอลัมน์หนึ่งคือ 10 0 จะถูกเขียน และ 1 ถูกส่งไปยังคอลัมน์ด้านซ้ายทันที ที่จะบวกเข้ากับผลรวมของทั้งสองบิตตรงนั้น เมื่อผลรวมเป็น 3 จะหมายถึง 11 ในฐาน 2 เขียน 1 ใน 11 ทางขวา และ 1 ทางซ้ายถูกยกไปบวกกับผลรวมของบิตของคอลัมน์ทางซ้ายทันที ไม่ว่าในกรณีใด ตัวที่ 1 ยกไปทางซ้ายเรียกว่าตัวยก
อ่านตารางบวกก่อนหน้าจากทางขวา ในคอลัมน์ที่สอง (จากขวา) มีการพกพาซึ่งเป็นผลมาจาก 1+1 = 10 ในคอลัมน์ที่สาม มีการพกพาซึ่งเป็นผลมาจาก 1+1+ ของ 1 = 11 ในคอลัมน์ที่สี่ มีการยกเป็นผลจาก 0+1+ การยกของ 1 = 10 ในคอลัมน์ที่ห้า ไม่มีการยกเนื่องจากผลรวมคือ 0+0+ การยกของ 1 = 1 คอลัมน์ที่เหลือไม่มีการยก
การนับคอลัมน์เริ่มจากด้านขวาสุด ด้วยการบวกแบบ 16 บิต จึงสามารถยกจากคอลัมน์ที่แปดไปยังคอลัมน์ที่เก้าได้ (เลื่อนไปทางซ้าย) ตารางต่อไปนี้แสดงให้เห็นสิ่งนี้:

การดำเนินการทางคณิตศาสตร์และลอจิกเกิดขึ้นในไมโครโปรเซสเซอร์บนเมนบอร์ดของคอมพิวเตอร์
สำหรับคอมพิวเตอร์เวิร์ด 8 บิต การพกพาไม่สามารถไปจากบิตที่แปดถึงบิตที่เก้าโดยอัตโนมัติโดยฮาร์ดแวร์ ดังนั้น ในการเพิ่มกลุ่ม 16 บิตสองกลุ่มในคอมพิวเตอร์ดังกล่าว จะต้องดำเนินการเพิ่มสองครั้งในคู่แปดถึงแปดบิต การพกพาถูกย้ายและได้รับผลกระทบจากซอฟต์แวร์ (การเขียนโปรแกรม)
หากต้องการบวกตัวเลขสองตัว ตัวเลขนั้นสามารถแปลงเป็นรูปแบบเสริมของสองตัวนั้นได้ก่อน (ดูด้านล่าง) ก่อนที่จะบวก
3.3 การเสริมสองและการลบเลขฐานสอง
บนเมนบอร์ดของคอมพิวเตอร์จะมีหน่วยความจำและมีไมโครโปรเซสเซอร์และวงจรอื่นๆ หน่วยความจำคือชุดของเซลล์แปดบิต สำหรับหนึ่งไบต์ แต่ละบิตจะเข้าไปในเซลล์ ไมโครโปรเซสเซอร์มีตำแหน่งประเภทหน่วยความจำไม่กี่ตำแหน่ง ตำแหน่งประเภทหน่วยความจำเหล่านี้เรียกว่ารีจิสเตอร์ ดังนั้นในคอมพิวเตอร์ กลุ่มของไบต์สามารถจัดเก็บไว้ชั่วคราวในหน่วยความจำหรือในรีจิสเตอร์ของไมโครโปรเซสเซอร์
ในที่เก็บข้อมูลเหล่านี้ แต่ละเซลล์สามารถมี 1 หรือ 0 ก็ได้ และไม่มีอย่างอื่นอีกเลย ในชีวิตมีทั้งเลขบวกและลบ จำนวนบวกเริ่มต้นด้วยเครื่องหมายบวก (+) และจำนวนลบเริ่มต้นด้วยเครื่องหมายลบ (-) เมื่อละเครื่องหมายไว้ จะถือว่าตัวเลขนั้นเป็นจำนวนบวก
เพื่อแก้ปัญหาการระบุเครื่องหมายของตัวเลขในคอมพิวเตอร์ ตัวเลขทั้งหมดจึงถูกจัดเก็บไว้ในช่วง จำนวนเต็มเป็นจำนวนเต็ม ถ้าใช้แปดบิตเพื่อเก็บช่วงของตัวเลขที่เป็นไปได้ บิตซ้ายสุดจะถูกใช้เป็นบิตเครื่องหมาย ถ้าตัวเลขขึ้นต้นด้วย 0 แสดงว่าตัวเลขนั้นเป็นจำนวนบวก ถ้าขึ้นต้นด้วย 1 แสดงว่าตัวเลขนั้นเป็นจำนวนลบ ถ้าใช้สิบหกบิตเพื่อเก็บช่วงของตัวเลขที่เป็นไปได้ บิตซ้ายสุดจะถูกใช้เป็นบิตเครื่องหมาย ถ้าตัวเลขขึ้นต้นด้วย 0 ตัวเลขนั้นจะเป็นจำนวนบวก ถ้าขึ้นต้นด้วย 1 แสดงว่าตัวเลขนั้นเป็นจำนวนลบ ตัวเลขในแบบฟอร์มนี้เรียกว่าตัวเลขที่ลงนาม
ในทางปฏิบัติ สามารถเซ็นชื่อตัวเลขได้ 8 บิต 16 บิต 32 บิต และ 64 บิต ยิ่งใช้จำนวนบิตกว้างขึ้นเท่าใด ช่วงของตัวเลขที่เป็นไปได้ที่สามารถจัดเก็บก็จะยิ่งมากขึ้นเท่านั้น
จำนวนเต็มเสริมของ Two
เมื่อใช้ส่วนเสริมสอง จำนวนบวกจะเป็นจำนวนนับปกติ ยกเว้นหลักซ้ายสุดคือ 0 หากต้องการได้จำนวนลบที่สอดคล้องกันสำหรับจำนวนบวกใดๆ ให้กลับบิตแต่ละบิตเป็นตัวเลขแล้วบวก 1 เข้ากับผลลัพธ์ การกลับหรือส่วนเสริมของ 0 คือ 1 การกลับหรือส่วนเสริมของ 1 คือ 0 ตารางต่อไปนี้แสดงตัวเลขส่วนเสริมของสองตัวในช่วง:
| ตารางที่ 3.31 จำนวนเต็มเสริมของ Two ในสองบิต |
|
|---|---|
| ไบนารี่ | ทศนิยม |
| 01 | +1 |
| 00 | +0 |
| สิบเอ็ด | -1 |
| 10 | -2 |
เลขฐานสองบวกคือ 00 และ 01 (นั่นคือศูนย์และหนึ่ง) ในบิตซ้ายสุด ศูนย์แสดงว่าเป็นจำนวนบวก 00 ค่อนข้างอยู่ในช่วงกลางของช่วง เพื่อให้ได้ -1 การกลับตัวของตัวเลข 01 จะเป็น 10 การบวก 1 เข้าไป (ทางด้านขวาสุด) จะได้ 11
เนื่องจากมีการใช้สองบิต จึงเหลือเพียงบิตเดียวเพื่อแสดงตัวเลขในช่วงซึ่งประกอบด้วยตัวเลข +1, +0 และ -1 ที่สอดคล้องกับ 01, 00 และ 11 บิตแรกระบุเครื่องหมาย มันบังเอิญว่า 10 สำหรับ +2 ไม่ได้อยู่ในเลขฐานสองทั้งสามนี้ 10 ขึ้นต้นด้วย 1 ซึ่งหมายความว่าต้องเป็นจำนวนลบในส่วนเติมเต็มของสอง ดังนั้น 10 จึงรวมอยู่ในพิสัยนี้ ซึ่งหมายถึง -2
ด้วยสองบิตในส่วนเสริมของสอง จำนวนจำนวนเต็มทั้งหมด (บวกและลบ) ที่สามารถแสดงได้คือ 2 2 = 4 ไม่ใช่ 2 2 -1 = 3 ความแตกต่างอันเป็นผลจากการบวกจำนวนลบตัวสุดท้ายซึ่งเป็นค่าลบของ 2 หมายเลขด้วย – 1. ในกรณีนี้ -2 2-1 = -2 1 = -2. ไม่มี +2 ในช่วงของตัวเลขเสริมของทั้งสองใน 2 บิต
| ตารางที่ 3.32 จำนวนเต็มเสริมของ Two ในสี่บิต |
|
|---|---|
| ไบนารี่ | ทศนิยม |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1,010 | -6 |
| 1001 | 1001 |
| 1,000 | -8 |
เลขฐานสองบวกคือตั้งแต่ 0000 ถึง 0111 (นั่นคือตั้งแต่ศูนย์ถึงเจ็ด) ในบิตซ้ายสุด ศูนย์แสดงว่าเป็นจำนวนบวก 0000 ค่อนข้างอยู่ในช่วงกลางของช่วง ในการรับ -1 การกลับด้านของตัวเลข 0001 จะพบว่าเป็น 1110 การบวก 1 ในส่วนนี้ (ที่ด้านขวาสุด) จะได้ 1111 หากต้องการรับ -2 การกลับด้านของ 0010 จะพบว่าเป็น 1101 การบวก 1 ในส่วนนี้ ( จากขวาสุด) ให้ 1110 ส่วนเลขฐานสองติดลบอื่นๆ เช่น -3 ถึง -7 ก็ถูกกำหนดในทำนองเดียวกัน
เนื่องจากใช้สี่บิต จึงเหลืออีกสามบิตเพื่อแสดงตัวเลขในช่วงคือ +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 และ -7 สอดคล้องกับ 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, 1010 และ 1001
-8 ซึ่งตรงกับ 1,000 จะต้องได้รับการแก้ไขแยกกัน บิตแรกของตัวเลขเหล่านี้ทั้งหมดระบุเครื่องหมายของ 0 สำหรับจำนวนบวก และ 1 สำหรับจำนวนลบ มันบังเอิญว่า 1,000 ไม่ได้อยู่ในเลขฐานสองทั้งสิบสี่นี้ 1,000 ขึ้นต้นด้วย 1 ซึ่งหมายความว่าต้องเป็นจำนวนลบ เท่าที่เกี่ยวข้องกับส่วนเสริมของสอง ดังนั้น 1,000 จึงรวมอยู่ในพิสัยนี้ ซึ่งก็คือ -8
ด้วยสี่บิตในส่วนเสริมของสอง จำนวนจำนวนเต็มทั้งหมด (บวกและลบ) ที่สามารถแสดงได้คือ 2 4 = 16 และไม่ใช่ 2 4 – 1 = 15 ความแตกต่างเป็นผลจากการบวกจำนวนลบตัวสุดท้ายที่เป็นลบของ 2 จำนวนความกว้าง – 1. ในกรณีนี้ -2 4 -1 = -2 3 = -8. ไม่มี +8 ในช่วงของตัวเลข
การวิเคราะห์ก่อนหน้านี้สำหรับสอง สี่ และบิตที่กว้างขึ้นในส่วนเสริมของสองสามารถนำไปใช้กับเลขฐานสองแบบกว้าง 8 บิต 16 บิต 32 บิต และ 64 บิต
ส่วนเสริมของทั้งสองจะเสียสละบิตแรก (ซ้ายสุด) สำหรับเครื่องหมาย 0 สำหรับจำนวนบวก และ 1 สำหรับจำนวนลบ สำหรับกลุ่มบิตที่มีความกว้าง “n” บิต จะมี 2 บิต n จำนวนบวกบวกลบทั้งหมด มันจะเป็น 2 n -1 ไม่ใช่เพราะจำนวนลบนำโชคสุดท้าย (น้อยที่สุด) ที่รวมอยู่ด้วย จำนวนบวกสูงสุดคือ +2 n-1 -1 และจำนวนลบที่น้อยที่สุดคือ -2 n-1 -1. มันจะเป็น -2 n-1 -1 ไม่ใช่เพราะผู้โชคดี -2 เหรอ n-1 รวมอยู่ด้วย.
การลบตัวเลขเป็นส่วนเสริมของเลขสอง
ในการลบ:
ก – ข = ง
A เรียกว่า minuend, B เรียกว่า subtrahend และ D เรียกว่า ผลต่าง
หากต้องการลบเลขฐานสองบวกหนึ่งตัวออกจากเลขฐานสองบวกอีกตัวหนึ่ง เครื่องหมาย minuend จะถูกเขียนเป็นส่วนเสริมของ two และตัวลบจะถูกแปลงเป็นค่าส่วนเสริมของตัวที่สองที่เป็นลบ ดังนั้น ประโยคทางคณิตศาสตร์จึงกลายเป็น:
เอ+ – ข = ง
กล่าวอีกนัยหนึ่ง ในการลบส่วนเสริมของ two เครื่องหมายลบจะถูกแปลงเป็นจำนวนลบแล้วบวกเข้ากับเครื่องหมาย minuend
ตัวอย่าง 3.31:
ประเมินนิพจน์ทศนิยมต่อไปนี้ในส่วนเสริมของสองโดยใช้สี่บิต:
6 – 4
สารละลาย:
เลขฐานสองสำหรับ 6 คือ 110 ในส่วนเสริมของ 2 บิตแบบ 4 บิต มันคือ 0110 เลขฐานสองสำหรับ +4 คือ 100 ในส่วนเสริมของ 2 แบบ 4 บิตคือ 0100 0100 ซึ่งจะต้องแปลงเป็นลบ 4 ในเลขสอง ส่วนเสริมหรือการผกผันของ 0100 คือ 1011 การบวก 1 จากด้านขวาสุดดังที่เราทำเพิ่มเติม จะได้ 1100 ดังนั้น นิพจน์ทศนิยมคือ:
6 – 4 ซึ่งกลายเป็น:
0110 – 0100 ซึ่งก็คือ
0110 +(– 0100) = 0110 + 1100 ทำตามในส่วนเพิ่มเติมก่อนหน้าเป็น:

หมายเหตุ: 0110 +(– 0100) มีค่าเท่ากับ 6 + – 4
ด้วยการลบส่วนเติมเต็มของทั้งสอง การบวกใดๆ ก็ตามหลังจากคอลัมน์สุดท้ายไปทางซ้าย นอกเหนือจากนั้น จะถูกโยนทิ้งไป เมื่อลบเป็นทศนิยม คำสั่งทางคณิตศาสตร์จะเป็นดังนี้:
6 – 4 = 2
การทำสิ่งเดียวกันในส่วนเติมเต็มของสอง คำตอบคือ 0010 ซึ่งเป็น +2 ในการนับไบนารีส่วนเสริมของสอง การลบครั้งก่อนจะลบจำนวนที่น้อยกว่าออกจากจำนวนที่มากกว่า ในตัวอย่างต่อไปนี้ จำนวนที่มากกว่าจะถูกลบออกจากจำนวนที่น้อยกว่า สามารถพิจารณาจากตาราง 3.32 เพื่อดูว่า 0010 เป็นส่วนเสริมของสองจริง ๆ ซึ่งเทียบเท่ากับ +2 หรือไม่
ตัวอย่าง 3.32:
ประเมินนิพจน์ทศนิยมต่อไปนี้ในส่วนเติมเต็มของสองด้วยสี่บิต:
4 – 6
สารละลาย:
เลขฐานสองสำหรับ 4 คือ 100 ในส่วนเติมเต็มของ 2 แบบ 4 บิต มันคือ 0100 เลขฐานสองสำหรับ +6 คือ 110 ในส่วนเติมเต็มของ 2 แบบ 4 บิต มันคือ 0110 0110 จะต้องถูกแปลงเป็นลบ 6 ในส่วนเติมเต็มของสอง ดังต่อไปนี้: ส่วนเสริมหรือการกลับกันของ 0110 คือ 1001 การบวก 1 จากด้านขวาสุดดังที่เราทำในการบวกครั้งก่อน จะได้ 1010 ดังนั้น นิพจน์ทศนิยมคือ:
4 – 6 ซึ่งกลายเป็น:
0100 – 0110 ซึ่งก็คือ
0100 +(– 0110) = 0100 + 1010 ทำตามในส่วนเพิ่มเติมก่อนหน้าเป็น:

หมายเหตุ: 4+ – 6 เหมือนกับ 0100 +(– 0110)
ด้วยการลบส่วนเติมเต็มของทั้งสอง การบวกใดๆ ก็ตามหลังจากคอลัมน์สุดท้ายไปทางซ้าย นอกเหนือจากนั้น จะถูกโยนทิ้งไป เมื่อลบเป็นทศนิยม คำสั่งทางคณิตศาสตร์จะเป็นดังนี้:
4 – 6 = -2
การทำสิ่งเดียวกันในส่วนเติมเต็มของสอง คำตอบคือ 1110 ซึ่งก็คือ -2 ในการนับไบนารีส่วนเสริมของสอง สามารถพิจารณาจากตาราง 3.32 เพื่อดูว่า 1110 เป็นส่วนเสริมของสองจริง ๆ ซึ่งเทียบเท่ากับ -2 หรือไม่
3.4 การคูณเลขฐานสอง
ในแถลงการณ์:
ก x ข = ป
A เรียกว่าตัวคูณ B เรียกว่าตัวคูณ และ P เรียกว่าผลคูณ นิพจน์ A x B หมายถึงการบวกจำนวน A, B ครั้งที่ A และ B เป็นจำนวนเต็ม (จำนวนเต็ม)
การคูณในไบนารี่จะเหมือนกับการคูณในทศนิยม อย่างไรก็ตาม แทนที่จะทำในรูปแบบทศนิยม กลับทำในรูปแบบไบนารี การคูณนิพจน์ทศนิยมของ 42 x 10 ทำได้ในรูปแบบไบนารี่ดังนี้ โดยที่ 42 10 = 101010 2 และ 10 10 = 1,010 2 : :
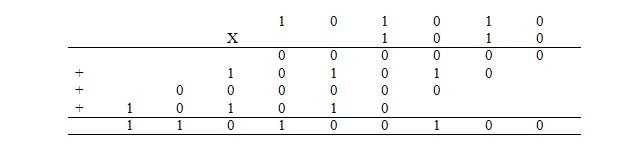
ตัวเลข 4 ตัวที่เพิ่มเข้ามาเรียกว่าผลคูณบางส่วน คำตอบก็คือผลิตภัณฑ์ การเพิ่มผลิตภัณฑ์บางส่วนทำได้ในลักษณะเดียวกับที่อธิบายไว้ก่อนหน้านี้
การคูณสามารถเห็นได้ดังนี้: ในการคูณฐานทั้งสองนี้ ถ้าบิต (หลัก) ในตัวคูณคือ 1 บิตที่มีนัยสำคัญน้อยที่สุดของผลิตภัณฑ์บางส่วนจะเป็นบิตที่มีนัยสำคัญน้อยที่สุดของตัวคูณซึ่งพิมพ์ซ้ำใต้บิตที่มีนัยสำคัญน้อยที่สุด และบิตที่เหลือของตัวคูณจะถูกทำซ้ำไปทางซ้าย ในการคูณฐานสองนี้ หากบิต (หลัก) ในตัวคูณคือ 0 ผลคูณบางส่วนของมันจะประกอบด้วย 0 โดยมีบิตที่มีนัยสำคัญน้อยที่สุดเป็น 0 อยู่ข้างใต้โดยตรง จำนวนศูนย์ทั้งหมดคือจำนวนบิตในตัวคูณ
3.5 การแบ่งเลขฐานสอง
ในแถลงการณ์:
ก ۞ B = คิว
A เรียกว่าเงินปันผล B เรียกว่าตัวหาร และ P เรียกว่าผลหาร ผลหารอาจมาพร้อมกับเศษ นิพจน์ A ÷ B หมายความว่าคุณสามารถเพิ่ม B เพื่อให้ A หรือใกล้เคียงกับ B ได้กี่ครั้ง โดยที่เศษเหลือเป็น 0 หรือน้อยกว่า B
การแบ่งสามารถทำได้หลายวิธี แผนกที่แสดงไว้นี้คือแผนกบูรณะ
แผนกฟื้นฟู
นี่เป็นวิธีการหารยาวที่เรียนกันในโรงเรียน ถ้า 237 หารด้วย 6 คำตอบคือ 39 เศษ 3. 237 10 ในฐาน 2 คือ 11101101 2 และ 6 10 ในฐาน 2 คือ 110 2 . 39 10 ในฐาน 2 คือ 100111 2 และ 3 10 ในฐาน 2 คือ 11 2 .
ดังนั้น 11101101 2 หารด้วย 110 2 ให้ 100111 2 ส่วนที่เหลือ 11 2 ในฐานสอง ด้วยวิธีการกู้คืน เลขฐานสองจะเป็นตัวเลขธรรมดาและไม่จำเป็นต้องเป็นส่วนเติมเต็มของทั้งสอง โครงสร้างต่อไปนี้แบ่ง 11101101 2 โดย 110 2 ให้ 100111 2 ส่วนที่เหลือ 11 2 : :

การลบทำได้ตามปกติและไม่ใช้ส่วนเติมเต็มของทั้งสอง เนื่องจากนี่คือฐานสอง การยืมจึงเป็นสองไม่ใช่สิบ เงินปันผลบางส่วนคือ 10, 101, 1,011, 1,010 และ 1,001 ส่วนที่เหลือคือ 11 เนื่องจากตัวหารมีตัวเลขสามหลัก โดยทั่วไปการหารจึงทำเป็นกลุ่มสามหลักจากเงินปันผลที่กำหนด ผลหารคือจำนวนเต็ม (จำนวนเต็ม) และสำหรับปัญหานี้คือ 100111 ผลลัพธ์ผลหารและเศษเป็นไปตามที่คาดไว้
3.6 การดำเนินการทางคณิตศาสตร์ด้วยซอฟต์แวร์และฮาร์ดแวร์
เมนบอร์ดคอมพิวเตอร์มีนาฬิกา เข็มนาฬิกาเรียกว่าพัลส์ ในแต่ละพัลส์นาฬิกา จะมีการตัดสินใจตั้งแต่หนึ่งรายการขึ้นไปในตำแหน่งที่แตกต่างกันบนเมนบอร์ด และนั่นก็คือเรื่องของการเขียนโปรแกรม (ซอฟต์แวร์)
ภายในไมโครโปรเซสเซอร์มีวงจรสองประเภทที่เรียกว่า: วงจรลอจิกเชิงผสม และ วงจรลอจิกตามลำดับ มีวงจรอีกประเภทหนึ่งที่เรียกว่ามัลติเพล็กเซอร์ การบวก การคูณ และการหารสามารถเกิดขึ้นได้ภายในหนึ่งช่วงสัญญาณนาฬิกาโดยใช้ตรรกะเชิงผสม (วงจร) ในขณะที่การเขียนโปรแกรม (ซอฟต์แวร์) กระทำการตัดสินใจที่พัลส์นาฬิกาแต่ละอันโดยใช้วงจรลอจิกซีเควนเชียลและมัลติเพล็กเซอร์
เมื่อการลบเสร็จสิ้นโดยใช้ส่วนเสริมของสอง จำเป็นต้องมีพัลส์นาฬิกาอย่างน้อยสองตัว ที่พัลส์นาฬิกาแรก มัลติเพล็กเซอร์จะแชนเนลย่อยไปยังชุดของ NOT เกต (หนึ่ง NOT เกตต่อหลัก) ที่พัลส์นาฬิกาที่สอง ลอจิกเชิงผสมจะเพิ่ม 1 ไปยังเอาต์พุตของเกต NOT และยังคงเพิ่มผลลัพธ์ส่วนย่อยและจุดสิ้นสุดต่อไป การเพิ่มทั้งหมดนั้นสามารถเกิดขึ้นได้ภายในหนึ่งช่วงสัญญาณนาฬิกา
การบวก การคูณ และการหารยังสามารถลดลงได้ด้วยการเขียนโปรแกรมโดยใช้ตารางความจริง อย่างไรก็ตาม ไม่ครอบคลุมอยู่ในหลักสูตรอาชีพออนไลน์นี้
3.7 การทำงานของลอจิกในไมโครโปรเซสเซอร์
และ, หรือ, XOR และกลับด้าน
และ
ตารางต่อไปนี้แสดง Bitwise AND ซึ่งหมายความว่าสำหรับเลขฐานสองที่แตกต่างกันสองตัว บิตที่สอดคล้องกันจะถูก ANDed ตามตาราง AND Truth:
เลื่อนจากซ้ายไปขวา 1 และ 1 = 1; 0 และ 1 = 0; 0 และ 0 = 0; 1 และ 0 = 0; และอื่นๆ ตามตารางความจริง AND
หรือ
ตารางต่อไปนี้แสดงให้เห็นถึง Bitwise OR ซึ่งหมายความว่าสำหรับเลขฐานสองที่แตกต่างกันสองตัว บิตที่สอดคล้องกันจะถูก ORed ตามตาราง OR Truth:

เลื่อนจากซ้ายไปขวา 1 หรือ 1 = 1; 0 หรือ 1 = 1; 0 หรือ 0 = 0; 1 หรือ 0 = 1; และอื่นๆ ตามตารางความจริงหรือ
ฟรี
ตารางต่อไปนี้แสดง Bitwise Exclusive-OR ซึ่งหมายความว่าสำหรับเลขฐานสองที่แตกต่างกันสองตัว บิตที่สอดคล้องกันจะถูก XORed ตามตาราง XOR Truth:

เลื่อนจากซ้ายไปขวา 1 XOR 1 = 0; 0 เอ็กซ์โออาร์ 1 = 1; 0 เอ็กซ์โอ 0 = 0; 1 เอ็กซ์โอ 0 = 1; และอื่นๆ ตามตารางความจริง XOR
กลับด้าน (ไม่ใช่)
ตารางต่อไปนี้แสดง Bitwise NOT (กลับด้าน) ซึ่งหมายความว่าสำหรับเลขฐานสองตัวหนึ่ง คราวนี้แต่ละบิตจะถูกกลับด้านตามตาราง NOT Truth:

เลื่อนจากซ้ายไปขวา ไม่ใช่ 1 = 0; ไม่ใช่ 0 = 1; ไม่ใช่ 0 = 1; ไม่ใช่ 1 = 0; และอื่นๆ ตามตาราง NOT Truth
ขยับไปทางขวาหรือซ้าย
เลื่อนไปทางขวา
เลขฐานสองต่อไปนี้ถูกเลื่อนตำแหน่ง 3 บิตไปทางขวา โดยมีเลขศูนย์แทรกอยู่ในตำแหน่งบิตที่ว่างทางด้านซ้าย:

การเปลี่ยนเกียร์สามารถทำได้ในหนึ่ง สอง สาม สี่ ฯลฯ
เลื่อนไปทางซ้าย
เลขฐานสองต่อไปนี้จะเลื่อนตำแหน่งบิตไปทางซ้าย 3 ตำแหน่ง โดยมีเลขศูนย์แทรกอยู่ในตำแหน่งบิตว่างทางด้านขวา:

การเปลี่ยนเกียร์สามารถทำได้ในหนึ่ง สอง สาม สี่ ฯลฯ
หมุนไปทางขวาหรือซ้าย
การหมุนก็คล้ายกับการขยับ มันทำทีละน้อย เมื่อหมุนไปทางขวา บิตที่ออกจากปลายด้านขวาจะไม่หลุดเหมือนการขยับ พวกมันจะแทนที่บิตที่ว่างทางด้านซ้ายทีละอัน เมื่อหมุนไปทางซ้าย บิตที่ออกจากปลายด้านซ้ายจะไม่หลุดเหมือนการขยับ พวกมันจะแทนที่บิตที่ว่างทางด้านขวาทีละอัน
หมุนไปทางขวา
เลขฐานสองต่อไปนี้ถูกหมุนไปทางขวา 3 ตำแหน่ง:

การหมุนสามารถทำได้ในหนึ่ง สอง สาม สี่ ฯลฯ
หมุนไปทางซ้าย
เลขฐานสองต่อไปนี้ถูกหมุนไปทางซ้าย 3 ตำแหน่ง:

การหมุนสามารถทำได้ในหนึ่ง สอง สาม สี่ ฯลฯ
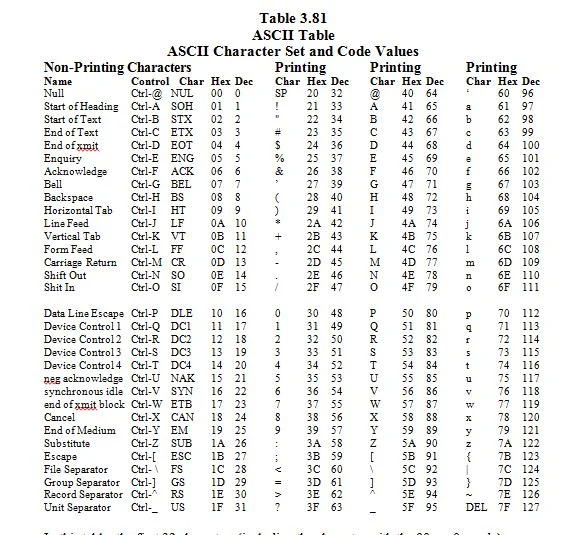
3.8 ชุดอักขระ ASCII และค่ารหัส
ASCII ย่อมาจาก 'รหัสมาตรฐานอเมริกัน (สหรัฐอเมริกา) สำหรับการแลกเปลี่ยนข้อมูล' ลองนึกภาพคีย์บอร์ดที่มี 96 คีย์ นี่คือแป้นพิมพ์ในอุดมคติที่ปุ่มตัวอักษรตัวพิมพ์ใหญ่แตกต่างจากปุ่มตัวอักษรตัวพิมพ์เล็ก ปุ่มอื่นๆ ทุกปุ่มแสดงถึงอักขระที่พบในแป้นพิมพ์ภาษาอังกฤษ (สหรัฐอเมริกา) อักขระและรหัส (ตัวเลขที่สอดคล้องกันสำหรับอักขระ) มีดังต่อไปนี้:
ในตารางนี้ อักขระ 32 ตัวแรก (รวมอักขระที่มี 00 16 = 0 10 code) เป็นอักขระที่ไม่พิมพ์ออกมา พวกเขาเป็นตัวละครควบคุม พวกเขาจะไม่เห็นบนหน้าจอ (จอภาพ) ซึ่งทุกอย่างเท่าเทียมกัน พวกมันมีผลเท่านั้น เราจะหารือเพิ่มเติมเกี่ยวกับเรื่องนั้นในภายหลัง
อักขระที่เหลือคืออักขระที่พิมพ์ พวกเขามองเห็นได้บนหน้าจอ มีอักขระ ASCII 128 ตัว 2 7 = 128.1,111,111 2 = 127 10 . 7อิน2 7 หมายถึง 7 บิต
ตอนนี้ 1111111 2 +1 2 เหมือนกับ:
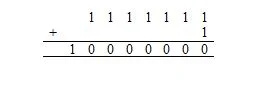
ที่นี่ 10,000,000 2 = 128 10 . มี 128 10 อักขระในรายการก่อนหน้า (ตาราง) ของอักขระ ASCII ซึ่งรวมถึงอักขระ null ซึ่งมีโค้ดในฐานสิบหก (เลขฐานสิบหก) คือ 00 ซึ่งเทียบเท่ากับ 0 ในฐานสิบ
เนื่องจากมีจำนวนอักขระทั้งหมด 128 ตัว อักขระที่ไม่พิมพ์ 128 ลบ 32 ตัวจึงได้อักขระที่พิมพ์ได้ 96 ตัว ในส่วนนี้ สันนิษฐานว่ามีแป้นพิมพ์ในอุดมคติที่มีอักขระ 96 ตัวซึ่งเป็นอักขระที่สามารถพิมพ์ได้ บนแป้นพิมพ์ในอุดมคตินี้ ปุ่มสำหรับอักขระภาษาอังกฤษตัวพิมพ์ใหญ่จะแตกต่างจากปุ่มของอักขระภาษาอังกฤษตัวพิมพ์เล็ก
อักขระแต่ละตัวบนแป้นพิมพ์จะแสดงด้วยเลขฐานสองจำนวน 7 บิตซึ่งไม่ได้แสดงอยู่ในรายการ ตัวอย่างเช่น ตัวอักษรตัวพิมพ์ใหญ่ของ “N” จะแสดงด้วยเจ็ดบิต 1001110 ในฐาน 2 วิธีแปลง 1001110 2 เป็นฐาน 16 นำหน้าด้วย 0 และจัดกลุ่มผลลัพธ์เป็นกลุ่มย่อยสี่บิตดังนี้
| 0100 | 1110 | 2 = | 4 | อี | 16
นั่นคือ 01001110 2 = 4อี 16 . ในการแปลง 4E 16 ถึงฐานสิบ ให้ทำดังต่อไปนี้:
4x(16) 1 + อี x (16) 0 = 4 x 16 + อ x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
ทางด้านขวาของ 'N' ในรายการ (ตาราง) คือเลขฐานสิบหกของ 4E และเลขฐานสิบของ 78
อีกตัวอย่างหนึ่ง อักขระ '[' จะแสดงด้วยเจ็ดบิต 1011011 ในฐาน 2 หากต้องการแปลง 1011011 2 เป็นฐาน 16 นำหน้าด้วย 0 และจัดกลุ่มผลลัพธ์เป็นกลุ่มย่อยสี่บิตดังนี้
| 0101 | 1011 | 2 = | 5 | บี | 16
นั่นคือ 01011011 2 = 5B 16 . หากต้องการแปลง 5B16 เป็นฐานสิบ ให้ทำดังนี้:
5x(16) 1 + ข x (16) 0 = 5 x 16 + ข x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
ทางด้านขวาของ '[' ในรายการ (ตาราง) คือเลขฐานสิบหก 5B และเลขฐานสิบ 91
อีกตัวอย่างหนึ่ง อักขระสำหรับเลขฐานสิบของ “5” จะแสดงด้วยเจ็ดบิต 0110101 ในฐาน 2 และ ไม่ 0000101 ในฐาน 2 เพื่อแปลง 0110101 2 เป็นฐาน 16 นำหน้าด้วย 0 และจัดกลุ่มผลลัพธ์เป็นกลุ่มย่อยสี่บิตดังนี้
| 0011 | 0101 | 2 = | 5 | บี | 16
นั่นคือ 00110101 2 = 35 16 . หากต้องการแปลง 3516 เป็นฐานสิบ ให้ทำดังนี้:
3 x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
ทางด้านขวาของ “5” ในรายการ (ตาราง) คือเลขฐานสิบหกคือ 35 และเลขฐานสิบคือ 53
เนื่องจากคอมพิวเตอร์ทำงานเป็นไบต์ เมื่อกดปุ่มบนแป้นพิมพ์ที่เหมาะสมที่สุด บิตแปดบิตจะถูกส่งไปยังไมโครโปรเซสเซอร์ (มาเธอร์บอร์ด) แป้นพิมพ์ในอุดมคติคืออุปกรณ์ต่อพ่วงที่แยกออกจากหน่วยระบบ (ฐาน) ของคอมพิวเตอร์ มีวงจรอิเล็กทรอนิกส์ (IC) ที่สร้างเจ็ดบิตและนำหน้าด้วยศูนย์ก่อนที่จะส่งผ่านสายเคเบิลไปยังมาเธอร์บอร์ดของยูนิตระบบ จากพอร์ตอินพุต (วงจรอินพุต) ของเมนบอร์ด ไปยังไมโครโปรเซสเซอร์ซึ่งอยู่บนเมนบอร์ดด้วย จากไมโครโปรเซสเซอร์จะไปยังหน่วยความจำที่ติดตั้งบนเมนบอร์ดด้วย
ดังนั้นเมื่อกดปุ่ม 'N' บนแป้นพิมพ์ในอุดมคติ บิตแปดบิต 01001110 จะถูกส่งไปยังไมโครโปรเซสเซอร์ จากไมโครโปรเซสเซอร์ พวกมันจะถูกส่งไปยังหน่วยความจำโดยที่พวกมันยังคงอยู่ในตำแหน่งหน่วยความจำเป็นไบต์ โปรแกรมเมอร์คอมพิวเตอร์ควรจำไว้ว่า 8 บิตคือ 01001110 2 ก็เหมือนกับ 4E 16 ซึ่งก็เหมือนกับ 78 10 .
เมื่อกดปุ่ม '[' บนแป้นพิมพ์ในอุดมคติ บิตแปด 01011011 จะถูกส่งไปยังไมโครโปรเซสเซอร์ จากไมโครโปรเซสเซอร์ พวกมันจะถูกส่งไปยังหน่วยความจำโดยที่พวกมันยังคงอยู่ในตำแหน่งหน่วยความจำเป็นไบต์ โปรแกรมเมอร์คอมพิวเตอร์ควรจำไว้ว่า 8 บิตคือ 01011011 2 ก็เหมือนกับ 5B 16 ซึ่งเหมือนกับ 91 10 .
เมื่อกดปุ่ม '5' บนแป้นพิมพ์ในอุดมคติ โดยเป็นอักขระและไม่ใช่เลขทศนิยม แปดบิต 00110101 จะถูกส่งไปยังไมโครโปรเซสเซอร์ จากไมโครโปรเซสเซอร์ พวกมันจะถูกส่งไปยังหน่วยความจำโดยที่พวกมันยังคงอยู่ในตำแหน่งหน่วยความจำเป็นไบต์ โปรแกรมเมอร์คอมพิวเตอร์ควรจำไว้ว่า 8 บิตคือ 00110101 2 ก็เหมือนกับ 35 16 ซึ่งเหมือนกับ 5310 10 .
มีหลายครั้งที่โปรแกรมกำลังทำงานและรอให้ป้อนเลขฐานสิบ 5 ลงในคอมพิวเตอร์ ในสถานการณ์นี้ หากกดปุ่ม '5' บนแป้นพิมพ์ในอุดมคติ รหัสแปดบิต 00110101 จะถูกส่งไปยังไมโครโปรเซสเซอร์ เนื่องจากสิ่งที่ต้องการคือเลขทศนิยม 5 ไม่ใช่อักขระ '5' โค้ดชิ้นหนึ่ง (โปรแกรมสั้น) จากหน่วยความจำจึงใช้ไมโครโปรเซสเซอร์ในการแปลงโค้ดอักขระ 00110101 ในฐานสองเป็นเลขเสริมของทั้งสอง 00000101 2 ก่อนที่จะส่งไปยังตำแหน่งหน่วยความจำเป็นไบต์เสริมของสอง โปรแกรมเมอร์คอมพิวเตอร์ต้องจำไว้ว่า 00000101 หมายถึง 5 10 ในฐาน 2 และแตกต่างจากรหัสตัวเลข 00110101 2 , 35 16 และ 53 10 ซึ่งหมายถึงอักขระของ '5' ในการแสดงหมายเลขเสริมของทั้งสองคือ 00000101 ในหน่วยความจำ โปรแกรมสั้นอีกโปรแกรมหนึ่งจะต้องแปลง 00000101 จากหน่วยความจำเป็น 00110101 ซึ่งก็คือ 00110101 ซึ่งมีค่าเท่ากับ 35 16 ซึ่งก็เหมือนกับปี 53 10 ที่แสดงบนจอภาพ (หรือพิมพ์บนกระดาษโดยเครื่องพิมพ์)
3.9 รูปแบบตัวเลขทศนิยม
ตัวเลขที่ไม่มีทศนิยมจะเป็นจำนวนเต็ม หมายเลข 36 เป็นจำนวนเต็ม 36.375 ไม่ใช่จำนวนเต็ม เป็นเลขทศนิยมที่มีส่วนทศนิยม ส่วนทศนิยมของ .375 เป็นเศษส่วนที่น้อยกว่า 1
36.375 ถูกตีความในรูปแบบทศนิยมดังนี้:
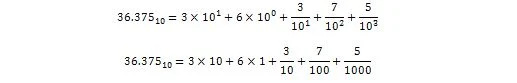
ตอนนี้:
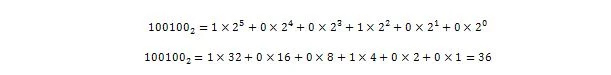
ดังนั้น 100100 2 = 3610 ซึ่งเป็นจำนวนเต็มของ 36.375 10 .
ตอนนี้:
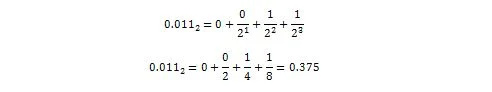
ดังนั้น 0.011 2 = 0.375 10 ซึ่งเป็นส่วนทศนิยมของ 36.375 10 .
∴ 36,375 10 = 100100.011 2
กล่าวอีกนัยหนึ่ง:
100100.011 2 = 36,375 10
ตัวเลขจะแสดงในคอมพิวเตอร์ในฐาน 2 ไม่ใช่ฐาน 10 โดยทุกอย่างจะเท่ากัน เนื่องจากเซลล์ในรีจิสเตอร์ในไมโครโปรเซสเซอร์หรือเซลล์ในหน่วยความจำสามารถรับค่าได้เพียง 1 หรือ 0 เท่านั้น จึงไม่มีที่ว่างสำหรับเก็บจุดทศนิยม สิ่งนี้ทำให้เกิดปัญหา ตามความละเอียด มีการแสดงจุดลอยตัว 32 บิตที่มีความแม่นยำเดี่ยว IEEE-754 และการแสดงจุดลอยตัว 64 บิตที่มีความแม่นยำสองเท่า IEEE-754
รูปแบบตัวเลขทศนิยม 32 บิต
หมายเลข 100100.0112 สามารถแสดงเป็น:
100100.011 2 = 1.00100011 2 x2 +5
ทางด้านขวามือของสัญลักษณ์ = ในทางคณิตศาสตร์เรียกว่าเป็นรูปแบบมาตรฐานฐานสองของด้านซ้ายมือของ 100100.011 2 .
ตอนนี้ 00100011 จาก 1.00100011 2 ที่ด้านขวามือของสัญลักษณ์ = โดยไม่มี “1” นำหน้า และไม่มีฐานเป็น 2 เรียกว่า นัยสำคัญโดยชัดแจ้ง ในกรณีนี้ จุดไบนารี่จะอยู่ทางซ้ายห้าตำแหน่งเพื่อให้มี “1” อย่าสับสนระหว่างจุดทศนิยมและจุดฐานสอง จุดไบนารี่สำหรับฐาน 2 ในขณะที่จุดทศนิยมสำหรับฐาน 10 “1” ตามด้วย 00100011 ทางด้านขวามือของสัญลักษณ์ = โดยไม่มีเลข 2 เป็นฐาน จะกลายเป็นนัยสำคัญที่แท้จริง อย่างไรก็ตาม 1.00100011 เรียกว่านัยสำคัญ
หลังเครื่องหมายทางขวามือคือ “x 2” +5 ' การแสดงออก. ด้วยนิพจน์นี้ +5 เรียกว่าเลขชี้กำลัง เครื่องหมายบวกหมายความว่าต้องย้ายจุดไบนารีไปข้างหน้าห้าตำแหน่งเพื่อให้อยู่ในตำแหน่งเดิมปกติ และ 2 เป็นฐานสำหรับการกำหนดหมายเลข สมการก่อนหน้าสามารถเขียนแบบย้อนกลับได้ดังนี้:
1.00100011 2 x2 +5 = 100100.011 2
ด้วยการแสดงจุดลอยตัวแบบ 32 บิต มันคือ “1.00100011 2 x2 +5 ” ที่ใช้และไม่ใช่แค่ “100100.011 2 '. 2 สำหรับฐานไม่ได้ถูกบันทึก การแสดงจุดลอยตัวแบบ 32 บิตสำหรับ “1.00100011 2 x2 +5 ” ซึ่งเท่ากับ 36.375 10 = 100100.011 2 ดังแสดงในตารางต่อไปนี้:

มีตำแหน่งแบบ 32 บิตซึ่งกำหนดหมายเลขจากปลายด้านขวา เริ่มต้นจาก 0 บิตแรกทางด้านซ้ายคือบิตเครื่องหมาย หากตัวเลขเป็นบวก บิตนี้จะเป็น 0 หากตัวเลขเป็นลบ บิตนี้จะเป็น 1 (-1 ประกอบด้วยอักขระสองตัว และไม่สามารถใส่ลงในเซลล์ใดเซลล์หนึ่งได้) 1.00100011 2 x2 +5 ซึ่งเท่ากับ 36.375 10 ซึ่งเท่ากับ 100100.011 เช่นกัน 2 เป็นจำนวนบวก ดังนั้นบิตแรกคือ 0
มีตำแหน่งบิตแปดตำแหน่งสำหรับเลขชี้กำลัง โดยเริ่มจากตำแหน่ง 30 ถึงตำแหน่ง 23 โดยรวม อย่างไรก็ตาม เลขยกกำลังที่เขียนไว้คือ 10000100 2 ซึ่งเท่ากับ 132 10 . เลขชี้กำลังของจำนวนดอกเบี้ยคือ +5 ของฐานสอง แล้วจะเกิดอะไรขึ้น?
ขณะนี้ในรูปแบบ 32 บิต เลขชี้กำลัง 0 จะเขียนเป็น 01111111 2 ซึ่งเท่ากับ 127 10 . +5 10 คือ +101 2 . ดังนั้นเมื่อถึง 10000100 2 ในส่วนเลขยกกำลังของตาราง 101 2 ถูกเพิ่มไปที่ 01111111 2 , ที่สอดคล้องกัน. หมายความว่า 5 ถูกบวกเข้ากับ 127 จึงมี 132 10 .
นัยสำคัญที่ไม่มี “1” เข้ามาแทนที่ตำแหน่ง 22 เหลือ 15 โดยรวม โปรดทราบว่า 1 ของ “1” ไม่ได้ระบุไว้ในสตริง 32 บิต ไม่เคยระบุ – ยอมรับสิ่งนั้น เซลล์ที่เหลือจนถึงตำแหน่ง 0 จะถูกเติมด้วยศูนย์
ถ้าเลขชี้กำลังจริงคือ -5 5 จะถูกลบออกจาก 127 10 มี 122 10 . นี่สอดคล้องกับการลบ 101 2 จาก 01111111 2 มี 01111010 2 .
จากภาพประกอบก่อนหน้านี้ทั้งหมด ตัวเลข +1 ซึ่งเท่ากับ 1.0 x 2 0 = 1.0 x 1 = 1.0 แสดงเป็น:

โปรดทราบว่า '1' ของ 1.0 x 2 0 ไม่ได้ระบุไว้ในรูปแบบ มันไม่เคยระบุไว้ เศษส่วนคละถัดไปที่เป็นบวกหลังจาก 1.0 คือ:

สังเกตเลข 1 ทางด้านขวาสุด. การแสดงนี้คือหมายเลข:

ความแตกต่างระหว่าง 1.0000001192092896 และ 1.0 คือ:
1.0000001192092896 – 1.0 = 0.0000001192092896
ตัวเลขที่มีทศนิยมเป็นเศษส่วนคละ ไม่ใช่เศษส่วนทั้งหมดระหว่าง 1 10 และ 2 10 สามารถแสดงผ่านคอมพิวเตอร์ได้ สันนิษฐานได้ว่าช่องว่างเศษส่วนที่เล็กที่สุดระหว่างตัวเลขคละที่ต่อเนื่องกันกับรูปแบบจุดลอยตัว 32 บิตคือ 0.0000001192092896 คาดว่าช่วงเวลาสำหรับความแม่นยำสองเท่าจะน้อยลง โปรดดูภาพประกอบต่อไปนี้
แทนตัวเลข 0.0 ไม่เป็นไปตามอาร์กิวเมนต์ก่อนหน้า มีการประกาศการเป็นตัวแทนของ 0.0 และจำเป็นต้องเรียนรู้เช่นนี้ หากต้องการแทน 0.0 เซลล์ทั้งหมดสำหรับซิกนิแคนด์จะเป็น 0 และเซลล์ทั้งหมดสำหรับเลขชี้กำลังจะเป็นศูนย์ด้วย บิตเครื่องหมายอาจเป็น 0 หรือ 1 ก็ได้ แต่น่าเสียดายที่สิ่งนี้ทำให้เกิดค่าบวก 0 และค่าลบ 0 ดังต่อไปนี้:

ในชีวิตจริงมีเพียงศูนย์เดียวเท่านั้น ไม่มีค่าบวก 0 และค่าลบ 0 อย่างไรก็ตาม โดยปกติแล้ว 0 จะถือเป็นค่าบวก ค่าบวก 0 และค่าลบ 0 อยู่ที่นี่เนื่องจากคำอธิบายรูปแบบเฉพาะนี้ เส้นจำนวน (ดูด้านบน) อาจมี +0 และ -0 ได้เช่นกัน แต่จะมีเพียงศูนย์เดียวเท่านั้น
รูปแบบตัวเลขทศนิยม 64 บิต
รูปแบบจุดลอยตัว 64 บิตคล้ายกับรูปแบบ 32 บิต แต่มีความแตกต่างดังต่อไปนี้:
- มี 64 บิตเพื่อแสดงตัวเลข
- หลังจากบิตเครื่องหมาย จะมี 11 บิตสำหรับเลขชี้กำลัง
- เลขชี้กำลังสำหรับดัชนีศูนย์ (2 0 ) คือ 1,023 10 = 01111111111 2 .
- สิบเอ็ดบิตตามด้วย 52 บิตสำหรับนัยสำคัญที่ชัดเจน
- มีช่วงตัวเลขที่กว้างกว่ารูปแบบ 32 บิต
โปรดทราบว่า '1' ที่อยู่ที่จุดเริ่มต้นของซิกนิฟิแคนด์ยังคงไม่รวมอยู่ใน 64 บิต เช่นเดียวกับที่ไม่รวมอยู่ใน 32 บิตสำหรับรูปแบบ 32 บิต
ความแตกต่างที่สำคัญที่สุดประการหนึ่งระหว่างรูปแบบ 64 บิตและรูปแบบ 32 บิตก็คือความแตกต่างระหว่างเศษส่วนผสมที่ต่อเนื่องกันในรูปแบบ 64 บิตนั้นมีขนาดเล็กกว่าของรูปแบบ 32 บิต
ในรูปแบบ 64 บิต ช่วงเวลา (ช่องว่าง) ระหว่าง 1.0 และเศษส่วนผสมถัดไปสามารถคำนวณได้ดังนี้:
1.0 คือ
0 01111111111 00000000000000000000 00000000000 000000000000000000000 2
ซึ่งเทียบเท่ากับ “1” ซึ่งไม่ได้ระบุไว้ในสตริง คูณด้วย 2 ยกกำลัง (ดัชนี) 0 (โดยมีเลขชี้กำลังเป็น 1023 10 = 01111111111 2 สำหรับ 2 0 = 1) สตริงคือ 1.0 x 2 0 .
เศษส่วนคละถัดไปที่มากกว่า 1.0 คือ:
0 01111111111 00000000000000000000 00000000000 00000000000000000001 2
ซึ่งเทียบเท่ากับ “1” ซึ่งไม่ได้ระบุไว้ในสตริง ตามด้วยศูนย์ 51 ตัว แล้ว 1 คูณด้วย 2 ยกกำลัง 0 (โดยมีเลขชี้กำลังเป็น 1023 10 = 011111111112 2 สำหรับ 2 0 = 1) นี่เป็นเช่นเดียวกับ:
+2 0 × (1 + 2− -52 ) data 1.0000000000000002
θ หมายถึงประมาณเท่ากับ
ตอนนี้:
1.0000000000000002 – 1.0 data 0.0000000000000002
ค่าช่วงเวลาที่สอดคล้องกันสำหรับรูปแบบ 32 บิตคือ 0.0000001192092896 data 0.00000012
0.0000000000000002 น้อยกว่า 0.00000012 มาก ดังนั้นจึงมีเศษส่วนผสมระหว่างจำนวนเต็มสองตัวติดต่อกัน (เช่น 3 และ 4) ในรูปแบบ 64 บิต มากกว่าที่มีระหว่างจำนวนเต็มสองตัวติดต่อกันสำหรับรูปแบบ 32 บิต
จำนวนเศษส่วนคละระหว่างจำนวนเต็มสองตัวติดต่อกันบนเส้นจำนวนนั้นไม่มีที่สิ้นสุด ดังนั้น ไม่มีรูปแบบใด (เช่น 32 บิตหรือ 64 บิต) ที่สามารถให้เศษส่วนแบบผสมทั้งหมดระหว่างจำนวนเต็มสองจำนวนติดต่อกัน (จำนวนเต็ม) ยิ่งช่องว่าง (ช่วงเวลา) ระหว่างจำนวนเต็มสองตัวติดต่อกันที่มีรูปแบบ (เช่น 32 บิตหรือ 64 บิต) น้อยลงเท่าใด จำนวนเศษส่วนผสมระหว่างจำนวนเต็มต่อเนื่องกันก็จะยิ่งมากขึ้นเท่านั้น (สำหรับเส้นจำนวน)
เหตุผลที่รูปแบบ 64 บิตถูกอธิบายว่ามีความแม่นยำเป็นสองเท่าหรือสูงกว่า เมื่อเปรียบเทียบกับรูปแบบ 32 บิต ก็คือช่วงเวลาระหว่างเศษส่วนผสมสองอันติดต่อกันที่ล้อมรอบด้วยจำนวนเต็มสองตัวติดต่อกันสำหรับรูปแบบ 64 บิตนั้นเล็กกว่า 32 ที่สอดคล้องกัน ช่วงเวลารูปแบบบิต นอกจากนี้ ยังมีเศษส่วนแบบผสมที่เป็นไปได้มากกว่าจำนวนเต็มที่มีขอบเขตสองตัวสำหรับรูปแบบ 64 บิต มากกว่าที่มีในรูปแบบ 32 บิตตามลำดับ
การแปลงส่วนทศนิยม (เศษส่วน) ของเลขทศนิยมให้เป็นส่วนไบนารี
36.375 เป็นเลขทศนิยมที่มีส่วนทศนิยมเป็น “.375” ส่วนทศนิยมของ “.375” คือเศษส่วนระหว่างศูนย์ถึงหนึ่ง 0.5 ในฐานสิบมีค่าเท่ากับ 1/2 ในฐานสอง 0.5 10 ที่แสดงด้วยส่วนขยายฐาน 2 คือ
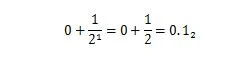
มันไม่ใช่ 0.101 2 ซึ่งหมายถึง 0.625 10 . ส่วนทศนิยมของเลขฐานสิบมีส่วนไบนารีที่เทียบเท่ากับเลขฐานสองที่สอดคล้องกัน ดังนั้นในการแปลงเลขทศนิยมเช่น 36.375 10 เป็นฐานสอง แปลง 36 เป็นไบนารี่ แล้วแปลง .375 เป็นไบนารี่ด้วย จากนั้นรวมผลลัพธ์ทั้งสองเข้ากับจุดไบนารี่ วิธีการแปลงทั้งสองส่วนจะแตกต่างกัน วิธีการแปลงจำนวนเต็มทศนิยมให้เป็นฐาน 2 มีอธิบายไว้ในบทที่ 1
หากต้องการแปลงเศษส่วนทศนิยมให้เป็นเศษส่วนไบนารี ให้ทำตามขั้นตอนต่อไปนี้:
- คูณเศษส่วนทศนิยม (ส่วนทศนิยม) ด้วย 2 จำนวนเต็มที่เป็นผลมาจากค่านี้คือเลขฐานสองตัวแรก
- ทำซ้ำขั้นตอนก่อนหน้าด้วยผลลัพธ์ทศนิยมที่เป็นเศษส่วนเพื่อให้ได้เลขฐานสองหลักถัดไป
- ทำซ้ำขั้นตอนก่อนหน้าต่อไปจนกว่าผลลัพธ์เศษส่วนทศนิยมจะเป็น .0000—
ตัวอย่าง: แปลงเศษส่วนของ 36.375 10 เป็นเศษส่วนที่เท่ากันในฐานสอง
สารละลาย:
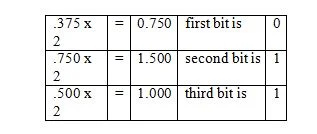
โปรดทราบว่าในขั้นตอนที่สาม .500 คูณด้วย 2 ไม่ใช่ 1.500 เศษส่วนที่สอดคล้องกันแบบไบนารีจะถูกอ่านที่คอลัมน์สุดท้ายจากด้านบน ดังนั้นผลลัพธ์ต่อไปนี้คือ:
.375 10 = .011 2
การแปลงส่วนไบนารี (เศษส่วน) ของเลขฐานสองให้เป็นส่วนทศนิยม
เพื่อให้บรรลุเป้าหมายนี้ ให้ขยายเศษส่วนไบนารี่ด้วยกำลังกลับของ 2
ตัวอย่าง: แปลงเศษส่วนของ 100100.011 2 เป็นเศษส่วนที่เท่ากันในฐานสิบ
สารละลาย:
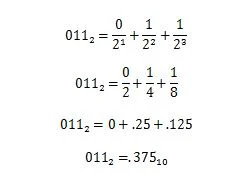
3.10 คำนำหน้าตัวเลขในคอมพิวเตอร์
ในชีวิตปกติ 1 กิโลหมายถึง 1,000 ซึ่งใช้อักษรย่อว่า k (ตัวพิมพ์เล็ก) เช่นเดียวกับ 1 กิโลกรัม ในการคำนวณ 1 กิโล หมายถึง 2 10 = 1024 แต่ใช้ตัวย่อเป็น K (ตัวพิมพ์ใหญ่) เช่นเดียวกับ 1Kbits ในชีวิตปกติ 1 เมกะ หมายถึง 1,000,000 ซึ่งใช้อักษรย่อ M (ตัวพิมพ์ใหญ่) เช่นเดียวกับ 1Mg ในการคำนวณ 1 เมกะหมายถึง 2 ยี่สิบ = 1,048,576 = 2 10 x2 10 = 1024 x 1024 = 1,048,576 และยังคงใช้อักษรย่อเป็น M (ตัวพิมพ์ใหญ่) เช่นเดียวกับ 1Mbits ในชีวิตปกติ 1 giga หมายถึง 1,000,000,000 จะใช้อักษรย่อว่า G (ตัวพิมพ์ใหญ่) เช่นเดียวกับ 1Gg ในการคำนวณ 1 กิกะหมายถึง 2 30 = 1,073,741,824 = 2 10 x2 10 x2 10 = 1024 x 1024 x 1024 = 1,073,741,824 และยังคงใช้อักษรย่อเป็น G (ตัวพิมพ์ใหญ่) เช่นเดียวกับใน 1Gbits ตารางต่อไปนี้ให้ความหมายของคำนำหน้าสี่คำในชีวิตปกติและในการคำนวณ:
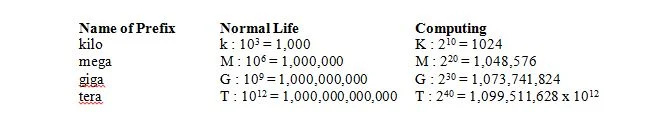
3.11 ปัญหา
ผู้อ่านควรแก้ไขปัญหาทั้งหมดในบทก่อนที่จะไปยังบทถัดไป
- วาดเส้นจำนวนด้วยจำนวนเต็มตั้งแต่ -10 ถึง +10
- เพิ่มเลขฐานสองต่อไปนี้ในส่วนเสริมสองของ 8 บิต: 101010 2 และ 1111 2 .
- ใช้เพียงวิธีเสริมของทั้งสองใน 8 บิตเพื่อลบเลขฐานสองของ 1111 2 จากเลขฐานสอง 101010 2 .
- ค้นหาผลิตภัณฑ์ของ 10110 2 x1101 2 ในฐานสอง
- หาร 36,375 10 ภายใน 1,000 10 เป็นทศนิยมและไบนารี่ แล้วเปรียบเทียบผลลัพธ์
- ใช้ 8 บิตที่คุณเลือกเพื่อแสดงตรรกะ AND, OR, XOR, Invert, Shift Right, Shift Left, Rotate Right และ Rotate Left แต่ละไบต์ควรมีส่วนผสมของ 1 และ 0
- ก) เขียนโค้ดตัวเลขสำหรับอักขระ ASCII ที่เป็นศูนย์ในรูปแบบเลขฐานสิบหก เลขฐานสอง และเลขฐานสิบ
b) เขียนรหัสตัวเลขสำหรับอักขระ ASCII ของ '1' ในเลขฐานสิบหก ไบนารี และทศนิยม
c) เขียนรหัสตัวเลขสำหรับอักขระ ASCII ของ 'A' ในเลขฐานสิบหก ไบนารี และทศนิยม
d) เขียนรหัสตัวเลขสำหรับอักขระ ASCII ของ 'a' ในเลขฐานสิบหก ไบนารี และทศนิยม - แปลง 49.49 10 เข้าไปในฐานสอง แปลงผลลัพธ์ของคุณเป็นรูปแบบจุดลอยตัว IEEE 32 บิต
- ก) รูปแบบจุดลอยตัวของ IEEE 64 บิตแตกต่างจากรูปแบบ 32 บิตอย่างไร
b) ให้เหตุผลสองประการที่เกี่ยวข้องว่าทำไมรูปแบบ 64 บิตจึงถูกอธิบายว่ามีความแม่นยำสองเท่าหรือสูงกว่า
รูปแบบ 32 บิต